Clase 12 Redes neuronales convolucionales
Las redes convolucionales son un tipo de arquitectura de red que utiliza ciertos supuestos acerca de los pesos, en contraste a las redes totalmente conexas donde los pesos pueden tomar cualquier valor. Esos supuestos están adaptados para explotar la estructura señales, por ejemplo: sonido, imágenes o texto En estos casos, se trata de entradas que tienen una estructura adicional de proximidad (es decir, hay un concepto de pixeles cercanos y lejanos, igual de tiempos cercanos o lejanos). Las redes convolucionales son una de las arquitecturas más exitosa para tratar con este tipo de problemas con estructura espacial o temporal.
Hay tres consecuencias básicos que se siguen del uso de convoluciones, que explicamos primero intuitivamente:
Conexiones ralas: existen unidades que solo están conectadas a una fracción relativamente chica de las unidades de la capa anterior (en lugar de todas, como en redes totalmente conexas). Por ejemplo: una unidad que busca detectar una forma en una esquina de una imagen no necesita estar conectada a pixeles de otras partes de la imagen.
Parámetros compartidos: diferentes unidades tienen pesos compartidos. Por ejemplo: una unidad que quiere detectar el sonido de cierto animal al principio de la grabación puede utilizar los mismos pesos aplicados a otra parte de la grabación. Podemos “mover” el detector (con los mismos pesos) a lo largo de la grabación para ver en dónde detecta el sonido que nos interesa.
Equivarianza: Una translación de una entrada (en tiempo o espacio), produce una traslación equivalente en la salida. Por ejemplo, Si una unidad asociada a la esquina superior derecha de una imagen detecta un número, entonces habrá otra unidad que puede detectar el número en la esquina inferior.
El éxito de este tipo de redes (como las convolucionales) está en encontrar la estructura apropiada para el problema que estamos tratando.
12.1 Filtros convolucionales
Filtros en una dimensión
Comenzamos por considerar filtros para una serie de tiempo.
Por ejemplo, consideramos la siguiente serie, y promedios móviles centrados de longitud 5. Los promedios móviles filtran las componentes de frecuencia alta (variaciones en tiempos cortos), y nos dejan con la variación de mayor frecuencia:
library(RcppRoll)
h <- function(x){ifelse(x>0, x, 0)}
datos <- tibble(t = 1:length(BJsales),
serie = as.numeric(BJsales) + rnorm(length(BJsales), 0, 10)) |>
mutate(promedio_mov = roll_mean(serie, 5, align='center', fill = NA))
ggplot(filter(datos, t < 100), aes(x=t, y=serie)) + geom_line() +
geom_line(aes(y=promedio_mov), colour='red', size=1.2)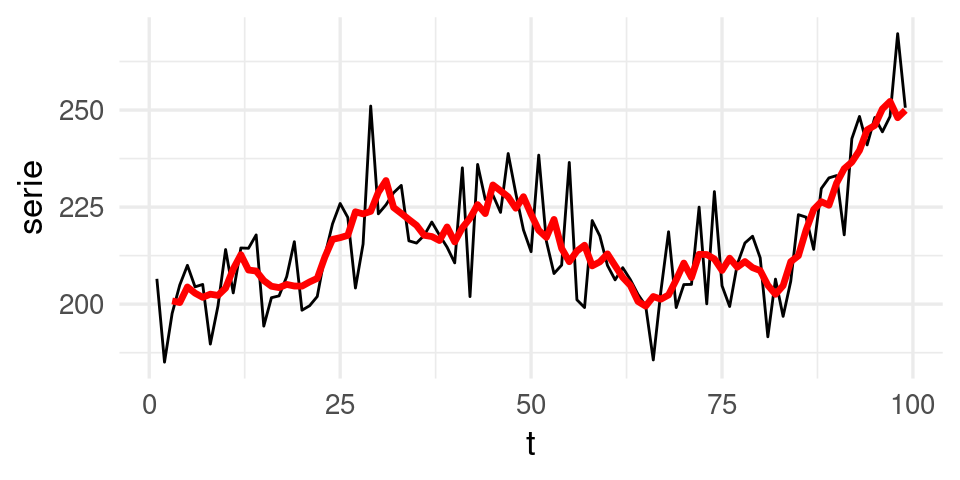
Podemos escribir este filtro de la siguiente manera: si \(x_t\) representa la serie original, y \(y_t\) la serie filtrada, entonces \[ y_t = \frac{1}{5}(x_{t-2} + x_{t-1} + x_t + x_{t+1}+x_{t+2})\]
Podemos escribir esta operación poniendo \[f =\frac{1}{5} (\ldots, 0,0,1,1,1,1,1,0,0,\ldots)\]
donde \(f_s=1/5\) para \(s=-2,-1,0,1,2\) y cero en otro caso.
Entonces \[y_t = \cdots + x_{t-2}f_{-2} + x_{t-1}f_{-1} + x_{t}f_{0} +x_{t+1}f_{1} +x_{t+2}f_{2}\] Que también se puede escribir como
\[y_t = \sum_{s=-\infty}^{\infty} x_s f_{s-t}\]
Nótese que estamos moviendo el filtro \(f\) a lo largo de la serie (tiempo) y aplicándolo cada vez.
Observación: en matemáticas y procesamiento de señales, la convolución es más comunmente \[y_t = \sum_{s=-\infty}^{\infty} x_s f_{t-s},\] mientras que la fórmula que nosotros usamos se llama correlación cruzada. En redes neuronales se dice filtro convolucional, aunque estrictamente usa la correlación cruzada (por ejemplo en Tensorflow).
Este es un ejemplo de filtro convolucional del tipo que se usa en redes neuronales: es un vector \(f\) que se aplica a la serie \(x\) como en la ecuación anterior para obtener una serie transformada (filtrada) \(y\). El vector se desplaza a lo largo de la serie par obtener los distintos valores filtrados.
12.2 Filtros convolucionales en dos dimensiones
En dos dimensiones, nuestro filtro es una matriz \(f_{i,j}\), que se aplica a una matriz \(x_{i,j}\) (podemos pensar que es una imagen) alrededor de cada posible pixel, para obtener la matriz (imagen) filtrada \(y_{i,j}\) dada por
\[y_{a,b} = \sum_{s,t=-\infty}^{\infty} x_{s,t} f_{s-a,t-b}\]
A la matriz \(f\) se le llama matriz convolucional, kernel o máscara del filtro.
Por ejemplo, consideremos el filtro de 3x3
filtro_difuminar <- matrix(rep(1 / 9, 9), 3, 3, byrow=T)
filtro_difuminar## [,1] [,2] [,3]
## [1,] 0.1111111 0.1111111 0.1111111
## [2,] 0.1111111 0.1111111 0.1111111
## [3,] 0.1111111 0.1111111 0.1111111El centro de este filtro se sobrepone sobre la cada pixel de la imagen \(x\), se multiplican los valores de la imagen por los del filtro y se suma para obtener el nuevo pixel de la imagen \(y\).
¿Qué efecto tiene este filtro? Este filtro promedia los pixeles de un parche de 3x3 de la imagen, o suaviza la imagen. Es el análogo en 2 dimensiones del filtro de promedios móviles que vimos arriba.
library(imager)
# leer imagen
estatua <- load.image('figuras/escultura.jpg') |> grayscale()
estatua_mat <- as.array(estatua)
dim(estatua_mat)## [1] 174 240 1 1# definir arreglo
estatua_dif <- array(0, c(dim(estatua)[1]-1, dim(estatua)[2]-1, 1, 1))
# Ojo: esta manera es muy lenta: si necesitas convoluciones a mano busca
# paquetes apropiados
for(i in 2:dim(estatua_dif)[1]){
for(j in 2:dim(estatua_dif)[2]){
estatua_dif[i, j, 1, 1] <- sum(filtro_difuminar * estatua[(i-1):(i+1), (j-1):(j+1), 1, 1])
}
}
plot(estatua, axes=FALSE)
plot(as.cimg(estatua_dif), axes=FALSE)
Podemos intentar otro filtro, que detecta bordes de arriba hacia abajo (es decir, cambios de intensidad que van de bajos a altos conforme bajamos en la imagen):
filtro_borde <- (matrix(c(-1, -1, -1, 0, 0, 0, 1, 1, 1), 3, 3, byrow=T))
filtro_borde## [,1] [,2] [,3]
## [1,] -1 -1 -1
## [2,] 0 0 0
## [3,] 1 1 1estatua_filtrada <- array(0, c(dim(estatua_dif)[1]-1, dim(estatua_dif)[2]-1, 1, 1))
for(i in 2:dim(estatua_filtrada)[1]){
for(j in 2:dim(estatua_filtrada)[2]){
estatua_filtrada[i,j,1,1] <- sum(t(filtro_borde)*estatua_dif[(i - 1):(i + 1),(j - 1):(j + 1), 1, 1])
}
}
plot(as.cimg(estatua_filtrada), axes = FALSE)
Este filtro toma valores altos cuando hay un gradiente de intensidad de arriba hacia abajo.
¿Cómo harías un filtro que detecta curvas? Considera el siguiente ejemplo, en donde construimos un detector de diagonales:
library(keras)
mnist <- dataset_mnist()
digito <- t(mnist$train$x[10,,])
plot(as.cimg(digito))
filtro_diag <- matrix(rep(-1,25), 5, 5)
diag(filtro_diag) <- 2
for(i in 1:4){
filtro_diag[i, i+1] <- 1
filtro_diag[i+1, i] <- 1
}
filtro_diag_1 <- filtro_diag[, 5:1]
filtro_diag_1## [,1] [,2] [,3] [,4] [,5]
## [1,] -1 -1 -1 1 2
## [2,] -1 -1 1 2 1
## [3,] -1 1 2 1 -1
## [4,] 1 2 1 -1 -1
## [5,] 2 1 -1 -1 -1digito_f <- array(0, c(dim(digito)[1]-2, dim(digito)[2]-2, 1, 1))
for(i in 3:dim(digito_f)[1]){
for(j in 3:dim(digito_f)[2]){
digito_f[i,j,1,1] <- sum((filtro_diag_1)*digito[(i-2):(i+2),(j-2):(j+2)])
}
}
plot(as.cimg(digito_f), axes = FALSE)
12.3 Filtros convolucionales para redes neuronales
En redes neuronales, la idea es que que qeremos aprender estos filtros a partir de los datos. La imagen filtrada nos da las entradas de la siguiente capa.
Entonces, supongamos que un filtro de 3x3 está dado por ciertos pesos
\[ f = \left[ {\begin{array}{ccccc} \theta_{1,1} & \theta_{1,2} & \theta_{1,3} \\ \theta_{2,1} & \theta_{2,2} & \theta_{2,3} \\ \theta_{3,1} & \theta_{3,2} & \theta_{3,3} \\ \end{array} } \right] \]
Este filtro lo aplicaremos a cada parche de la imagen de entrada. Empezamos aplicando el filtro sobre la parte superior izquierda de la imagen para calcular la primera unidad de salida \(a_1\)
knitr::include_graphics('./figuras/conv_1.png')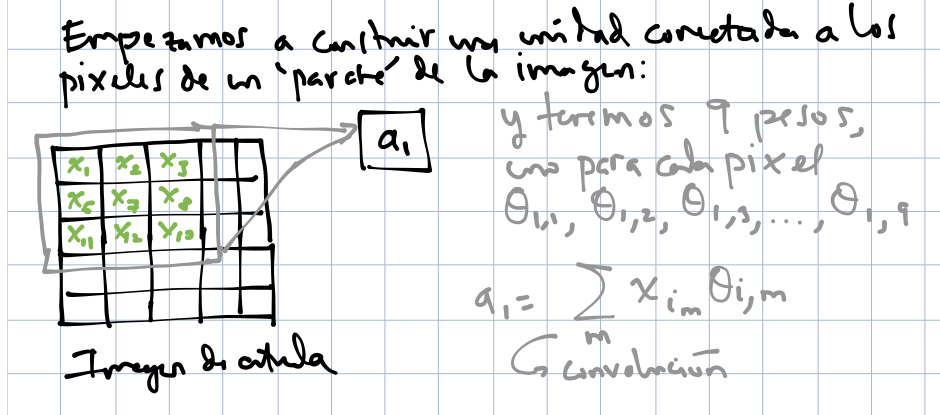
Ahora nos movemos un pixel a la derecha y aplicamos el filtro para obtener la unidad \(a_2\). Podemos poner las unidades en el orden de la imagen para entender mejor las unidades:
knitr::include_graphics('./figuras/conv_2.png')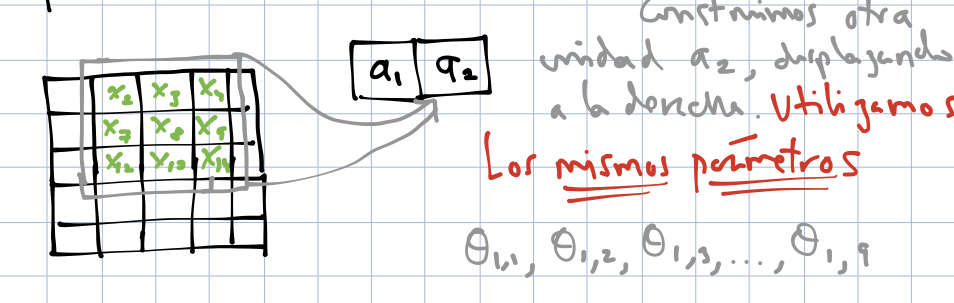
Al aplicar el filtro a lo largo de toda la imagen, obtenemos 9 unidades de salida:
knitr::include_graphics('./figuras/conv_3.png')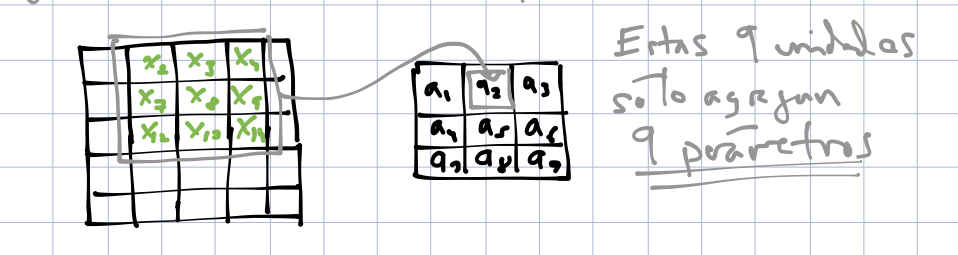
Finalmente, podemos agregar más parámetros para otros filtros:
knitr::include_graphics('./figuras/conv_4.png')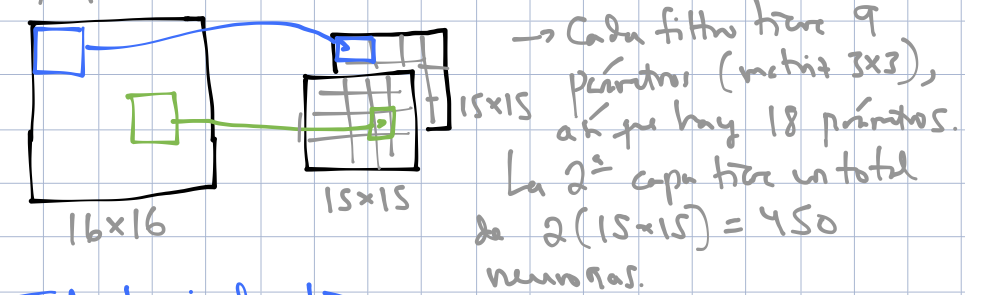
12.4 Capas de agregación
En procesamiento de imágenes y redes convolucionales también se utilizan capas de pooling. Estas se encargan de resumir pixeles adyacentes. Una de las más populares es el max pooling, donde en cada parche de la imagen tomamos el máximo.
knitr::include_graphics('./figuras/pooling_1.png')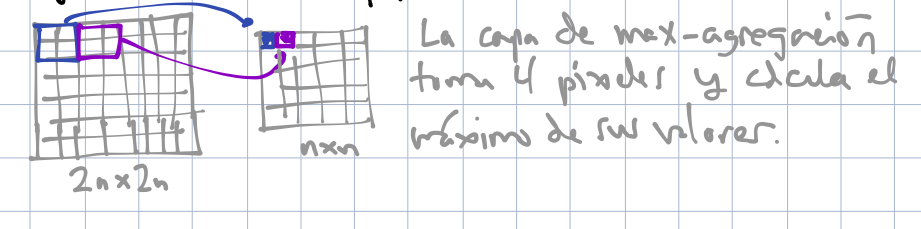
Hay dos razones para usar estas agregaciones:
- Obtener invarianza a translaciones adicional (en un parche de la imagen, solo importa si alguno de las unidades agregadas está activa para que el max-pooling esté activo)
- Reduce el tamaño de la imagen (o de una capa de convolución) y en consecuencia tenemos menos parámetros que tratar en las siguientes capas
12.5 Capas convolucionales más profundas.
Después de hacer una primera capa convolucional como la mostrada arriba, tendremos \(k\) imágenes filtradas, si utilizamos \(k\) filtros. Podemos pensar que tenemos estas \(k\) imágenes apiladas una encima de otra. Las siguientes capas convolucionales filtran la imágenes de esta pila (cada imagen filtrada tiene \(k\) componentes).
Un filtro en la siguiente capa actúa sobre todas las componentes de la capa anterior, así que consiste de:
- Un juego de pesos (por ejemplo de 5x5) para cada una de las \(k\) imágenes filtradas (\(5\times5\times k\) nuevos filtros).
- Después de aplicar estos pesos a cada imagen filtrada correspondiente, sumamos pixel a pixel para obtener una nueva imagen filtrada.
- Sumamos un sesgo.
Si esta segunda capa convolucional tiene \(m\) filtros, entonces obtendremos \(m\) imágenes filtradas.
12.6 Ejemplo: lector de medidor
Las capas de pooling generalmente se aplican después de las convoluciones, y hacia al final usamos capas totalmente conexas. Estas últimas capas se encargan de combinar la información de las capas de convolución anteriores, que detectan patrones simples, para obtener unidades que se encargan de detectar patrones más complejos.
Ahora regresamos a nuestro ejemplo introductorio de lectura de imágenes de medidor:
library(keras)
path_full_imgs <- list.files("../datos/medidor/", full.names = TRUE)
imagenes <- map(path_full_imgs, ~ image_load(.x, target_size = c(64, 64)))
imgs_array <- imagenes |> map(~ image_to_array(.x))
imgs_array <- map(imgs_array, ~ array_reshape(.x, c(1, 64, 64, 3)))
x <- abind::abind(imgs_array, along = 1)
path_imgs <- list.files("../datos/medidor/", full.names = FALSE)
y <- path_imgs |> str_sub(1, 3) |> as.numeric()
set.seed(2311)
# seleccionamos muestra de entrenamiento
indices_entrena <- sample(1:dim(x)[1], size = 4200)# generar minilotes de datos de las imágenes originales para entrenar
generador_1 <- image_data_generator(
rescale = 1/255,
rotation_range = 5,
zoom_range = 0.05,
horizontal_flip = FALSE,
vertical_flip = FALSE,
fill_mode = "nearest"
)
generador_entrena <- flow_images_from_data(
x = x[indices_entrena,,,],
y = y[indices_entrena] / 10,
generator = generador_1,
shuffle = TRUE,
batch_size = 32
)Mostramos algunos ejemplos del proceso generador de datos perturbados que acabamos de crear:
datos_entrena <- generator_next(generador_entrena)
op <- par(mfrow = c(2,2), pty = 's', mar = c(1, 0, 1, 0))
for (i in 1:4) {
aug_img <- datos_entrena[[1]]
plot(as.raster(aug_img[i, , , ]))
}
10 * datos_entrena[[2]][1:4]## [1] 2.6 9.3 6.0 2.1Y ahora construimos nuestra red convolucional:
modelo <- keras_model_sequential() |>
layer_conv_2d(input_shape = c(64, 64, 3), filters = 32, kernel_size = c(5, 5)) |>
layer_max_pooling_2d(pool_size = c(2, 2)) |>
layer_conv_2d(filters = 32, kernel_size = c(5, 5)) |>
layer_max_pooling_2d(pool_size = c(2, 2)) |>
layer_conv_2d(filters = 16, kernel_size = c(3, 3)) |>
layer_max_pooling_2d(pool_size = c(2, 2)) |>
layer_flatten() |>
layer_dropout(0.2) |>
layer_dense(units = 100, activation = "sigmoid") |>
layer_dropout(0.2) |>
layer_dense(units = 1, activation = 'linear')Podemos examinar el número de parámetros total y en cada capa (asegúrate que puedes contar los parámetros a mano con la especificación de arriba):
modelo## Model
## Model: "sequential"
## ________________________________________________________________________________
## Layer (type) Output Shape Param #
## ================================================================================
## conv2d_2 (Conv2D) (None, 60, 60, 32) 2432
## ________________________________________________________________________________
## max_pooling2d_2 (MaxPooling2D) (None, 30, 30, 32) 0
## ________________________________________________________________________________
## conv2d_1 (Conv2D) (None, 26, 26, 32) 25632
## ________________________________________________________________________________
## max_pooling2d_1 (MaxPooling2D) (None, 13, 13, 32) 0
## ________________________________________________________________________________
## conv2d (Conv2D) (None, 11, 11, 16) 4624
## ________________________________________________________________________________
## max_pooling2d (MaxPooling2D) (None, 5, 5, 16) 0
## ________________________________________________________________________________
## flatten (Flatten) (None, 400) 0
## ________________________________________________________________________________
## dropout_1 (Dropout) (None, 400) 0
## ________________________________________________________________________________
## dense_1 (Dense) (None, 100) 40100
## ________________________________________________________________________________
## dropout (Dropout) (None, 100) 0
## ________________________________________________________________________________
## dense (Dense) (None, 1) 101
## ================================================================================
## Total params: 72,889
## Trainable params: 72,889
## Non-trainable params: 0
## ________________________________________________________________________________modelo_aguja |> compile(
loss = "mse",
optimizer = optimizer_adam(lr = 0.001),
metrics = c('mae')
)
# Entrenar: nota es necesario correrlo más épocas, al menos 80-100
historia <- modelo_aguja |> fit(
generador_entrena,
epochs = 20,
verbose = TRUE,
validation_data = list(x = x[-indices_entrena,,,],
y = y[-c(indices_entrena)] / 10)
)
#write_rds(historia, "cache/historia-modelo-aguja.rds")
#save_model_hdf5(modelo_aguja, "cache/modelo-aguja.h5")modelo <- load_model_hdf5("cache/modelo-aguja.h5")Nótese que en este caso el error de validación es más bajo que el de entrenamiento: esto se debe en este ejemplo a que los errores de validación incluyen el dropout (promediando resultados de cada minilote) y las imágenes aumentadas, mientras que en validación usamos la red completa con las imágenes originales.
historia <- read_rds("cache/historia-modelo-aguja.rds")
plot(historia, smooth = FALSE) + geom_line()
El error de entrenamiento tiende a ser más alto que el de validación por el hecho
de que en entrenamiento sólo utilizamos la red con dropout, mientras que en validación
usamos la red completa. Adicionalmente, los datos de evaluación son los originales,
mientras que los de entrenamiento tienen las perturbaciones de nuestro proceso de aumentación.
score <- modelo |> evaluate(x[-indices_entrena,,,], y[-c(indices_entrena)] / 10)
score## loss mean_absolute_error
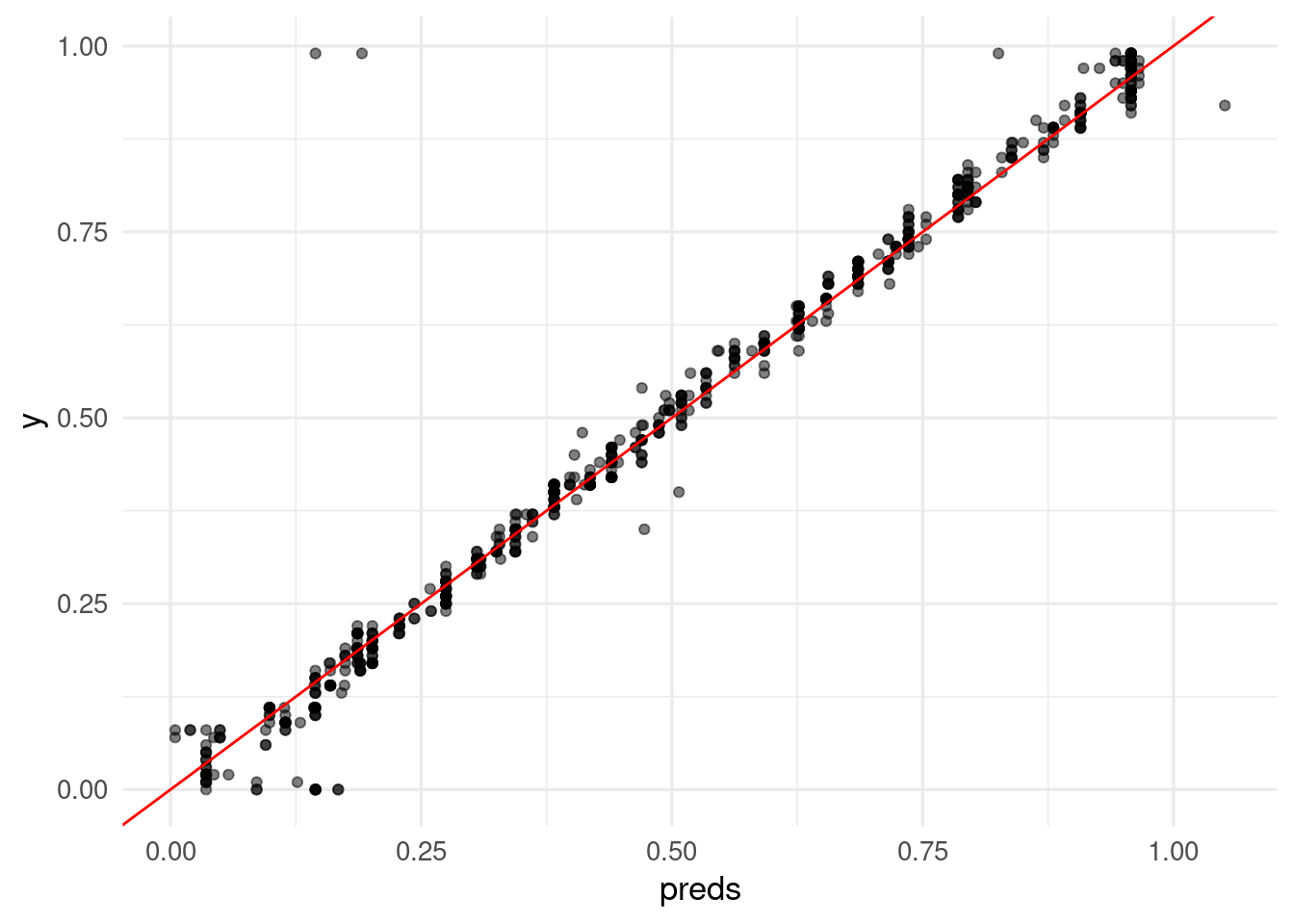
## 0.002577562 0.019456135preds <- predict(modelo, x[-indices_entrena,,,])
preds_tbl <- tibble(y = y[-c(indices_entrena)] / 10, preds = preds)
ggplot(preds_tbl, aes(x = preds, y = y)) +
geom_point(alpha = 0.5) +
geom_abline(colour = 'red')