Clase 19 Apéndice: Descenso en gradiente para regresión logística
Ahora veremos cómo aprender los coeficientes de regresión logística con una muestra de entrenamiento. La idea general es :
- Usamos la pérdida logarítmica de entrenamiento como medida de ajuste
- Usamos descenso en gradiente para minimizar esta pérdida y aprender los coeficientes.
Sea entonces \({\mathcal L}\) una muestra de entrenamiento:
\[{\mathcal L}=\{ (x^{(1)},y^{(1)}),(x^{(2)},y^{(2)}), \ldots, (x^{(N)}, y^{(N)}) \}\]
Donde \(y=1\) o \(y=0\) son las dos clases. Escribimos también
\[p_1(x)=p_1(x;\beta)= h(\beta_0+\beta_1x_1 + \beta_2x_2 +\cdots + \beta_p x_p),\]
y definimos la pérdida logarítmica sobre el conjunto de entrenamiento
\[D(\beta) = -\frac{1}{N}\sum_{i=1}^N \log(p_{y^{(i)}} (x^{(i)})).\]
Los coeficientes estimados por regresión logística están dados por \[\hat{\beta} = \arg\min_\beta D(\beta)\]
Para minimizar utilizaremos descenso en gradiente (aunque hay más opciones).
La última expresión para \(D(\beta)\) puede ser difícil de operar, pero podemos reescribir como: \[D(\beta) = -\frac{2}{N}\sum_{i=1}^N y^{(i)} \log(p_{1} (x^{(i)})) + (1-y^{(i)}) \log(p_{0} (x^{(i)})).\]
Para hacer descenso en gradiente, necesitamos encontrar \(\frac{\partial D}{\beta_j}\) para \(j=1,2,\ldots,p\).
Comenzamos por calcular la derivada de un término:
\[D^{(i)} (\beta) = y^{(i)} \log(p_{1} (x^{(i)})) + (1-y^{(i)}) \log(1-p_{1} (x^{(i)}))\]
Calculamos primero las derivadas de \(p_1 (x^{(i)};\beta)\) (demostrar la siguiente ecuación): \[\frac{\partial p_1}{\partial \beta_0} = {p_1(x^{(i)})(1-p_1(x^{(i)}))},\] y \[\frac{\partial p_1}{\partial \beta_j} = p_1(x^{(i)})(1-p_1(x^{(i)}))x_j^{(i)},\]
Así que \[\begin{align*} \frac{\partial D^{(i)}}{\partial \beta_j} &= \frac{y^{(i)}}{(p_1(x^{(i)}))}\frac{\partial p_1}{\partial \beta_j} - \frac{1- y^{(i)}}{(1-p_1(x^{(i)}))}\frac{\partial p_1}{\partial \beta_j} \\ &= \left( \frac{y^{(i)} - p_1(x^{(i)})}{(p_1(x^{(i)}))(1-p_1(x^{(i)}))} \right )\frac{\partial p_1}{\partial \beta_j} \\ & = \left ( y^{(i)} - p_1(x^{(i)}) \right ) x_j^{(i)} \\ \end{align*}\]
para \(j=0,1,\ldots,p\), usando la convención de \(x_0^{(i)}=1\). Podemos sumar ahora sobre la muestra de entrenamiento para obtener
\[ \frac{\partial D}{\partial\beta_j} = - \frac{1}{N}\sum_{i=1}^N (y^{(i)}-p(x^{(i)}))x_j^{(i)}\]
De modo que,
Podríamos usar las siguientes implementaciones, que representan cambios menores de lo que hicimos en regresión lineal. En primer lugar, escribimos la función que calcula la log pérdida. Podríamos poner:
log_perdida_calc_simple <- function(x, y){
log_perdida_fun <- function(beta){
p_beta <- h(as.matrix(cbind(1, x)) %*% beta)
- mean(y*log(p_beta) + (1-y)*log(1-p_beta))
}
log_perdida_fun
}*Observación Sin embargo, podemos hacer una simplificación para tener mejor desempeño y estabilidad. Observamos que \[\log (p_1(x;\beta)) = \log\frac{ e^{x^t \beta}}{1+ e^{x^t\beta}} = x^t\beta - \log Z\] donde \(Z = 1+ e^{x^t\beta}\). Por otra parte \[\log(p_0(x;\beta)) = \log\frac{ 1}{1+ e^{x^t\beta}} = - \log Z\] De modo que \[y\log(p_1(x;\beta)) + (1- y)\log(p_0(x;\beta)) = yx^t\beta - \log Z= yx^t\beta - \log (1+e^{x^t\beta})\] Así que podemos escribir:
log_perdida_calc <- function(x, y){
dev_fun <- function(beta){
x_beta <- as.matrix(cbind(1, x)) %*% beta
- mean(y * x_beta - log(1 + exp(x_beta)))
}
dev_fun
}Y para el gradiente
grad_calc <- function(x_ent, y_ent){
salida_grad <- function(beta){
N <- nrow(x_ent)
p_beta <- h(as.matrix(cbind(1, x_ent)) %*% beta)
e <- y_ent - p_beta
grad_out <- - (1 / N) * as.numeric(t(cbind(1,x_ent)) %*% e)
names(grad_out) <- c('Intercept', colnames(x_ent))
grad_out
}
salida_grad
}
descenso <- function(n, z_0, eta, h_deriv){
z <- matrix(0,n, length(z_0))
z[1, ] <- z_0
for(i in 1:(n-1)){
z[i+1, ] <- z[i, ] - eta * h_deriv(z[i, ])
}
z
}Ejemplo
Probemos nuestros cálculos con el ejemplo de 1 entrada de tarjetas de crédito.
p_1 <- function(x){
ifelse(x < 0.15, 0.95, 0.95 - 0.7 * (x - 0.15))
}
h <- function(z) { 1 / ( 1 + exp(-z))}
simular_impago <- function(n = 500){
# suponemos que los valores de x están concentrados en valores bajos,
# quizá la manera en que los créditos son otorgados
clases <- c("al_corriente", "impago")
x <- pmin(rexp(n, 100 / 40), 1)
# las probabilidades de estar al corriente:
prob <- p_1(x)
# finalmente, simulamos cuáles clientes siguen al corriente y cuales no:
g <- map_chr(1:length(x), ~ sample(clases, size = 1, prob = c(prob[.x], 1- prob[.x])))
g <- factor(g, levels = c("al_corriente", "impago"))
datos <- tibble(x = x, p_1 = prob, g = g) |>
mutate(y = ifelse(g == "al_corriente", 1, 0))
datos
}
set.seed(193)
dat_ent <- simular_impago() |> select(x, g, y)
dat_ent |> sample_n(20)## # A tibble: 20 × 3
## x g y
## <dbl> <fct> <dbl>
## 1 0.118 al_corriente 1
## 2 0.109 al_corriente 1
## 3 0.444 al_corriente 1
## 4 0.153 al_corriente 1
## 5 0.100 al_corriente 1
## 6 0.0109 al_corriente 1
## 7 0.216 al_corriente 1
## 8 1 impago 0
## 9 0.0846 al_corriente 1
## 10 0.144 al_corriente 1
## 11 0.377 impago 0
## 12 0.0908 al_corriente 1
## 13 0.128 al_corriente 1
## 14 0.00262 al_corriente 1
## 15 0.411 al_corriente 1
## 16 0.545 al_corriente 1
## 17 0.402 al_corriente 1
## 18 0.0544 al_corriente 1
## 19 0.00265 al_corriente 1
## 20 0.0927 al_corriente 1dat_ent <- dat_ent |> ungroup() |> mutate(x_s = (x - mean(x))/sd(x))
log_perdida <- log_perdida_calc(dat_ent[, 'x_s', drop = FALSE], dat_ent$y)
grad <- grad_calc(dat_ent[, 'x_s', drop = FALSE], dat_ent$y)
grad(c(0,1))## Intercept x_s
## -0.2889566 0.3990662grad(c(0.5,-0.1))## Intercept x_s
## -0.1538118 0.1663577Podemos verificamos el cálculo de gradiente usando una aproximación numérica
(log_perdida(c(0.5+0.0001,-0.1)) - log_perdida(c(0.5,-0.1)))/0.0001## [1] -0.1538001(log_perdida(c(0.5,-0.1+0.0001)) - log_perdida(c(0.5,-0.1)))/0.0001## [1] 0.1663696Y hacemos descenso:
iteraciones <- descenso(1000, z_0 = c(0,0), eta = 0.1, h_deriv = grad)
tail(iteraciones, 20)## [,1] [,2]
## [981,] 1.505927 -1.056649
## [982,] 1.505928 -1.056650
## [983,] 1.505928 -1.056650
## [984,] 1.505929 -1.056651
## [985,] 1.505930 -1.056651
## [986,] 1.505930 -1.056652
## [987,] 1.505931 -1.056652
## [988,] 1.505932 -1.056653
## [989,] 1.505933 -1.056653
## [990,] 1.505933 -1.056654
## [991,] 1.505934 -1.056654
## [992,] 1.505935 -1.056655
## [993,] 1.505935 -1.056655
## [994,] 1.505936 -1.056656
## [995,] 1.505937 -1.056656
## [996,] 1.505937 -1.056657
## [997,] 1.505938 -1.056657
## [998,] 1.505939 -1.056658
## [999,] 1.505939 -1.056658
## [1000,] 1.505940 -1.056658#Checamos devianza
qplot(1:nrow(iteraciones), apply(iteraciones, 1, log_perdida)) +
xlab("Iteración") + ylab("Devianza")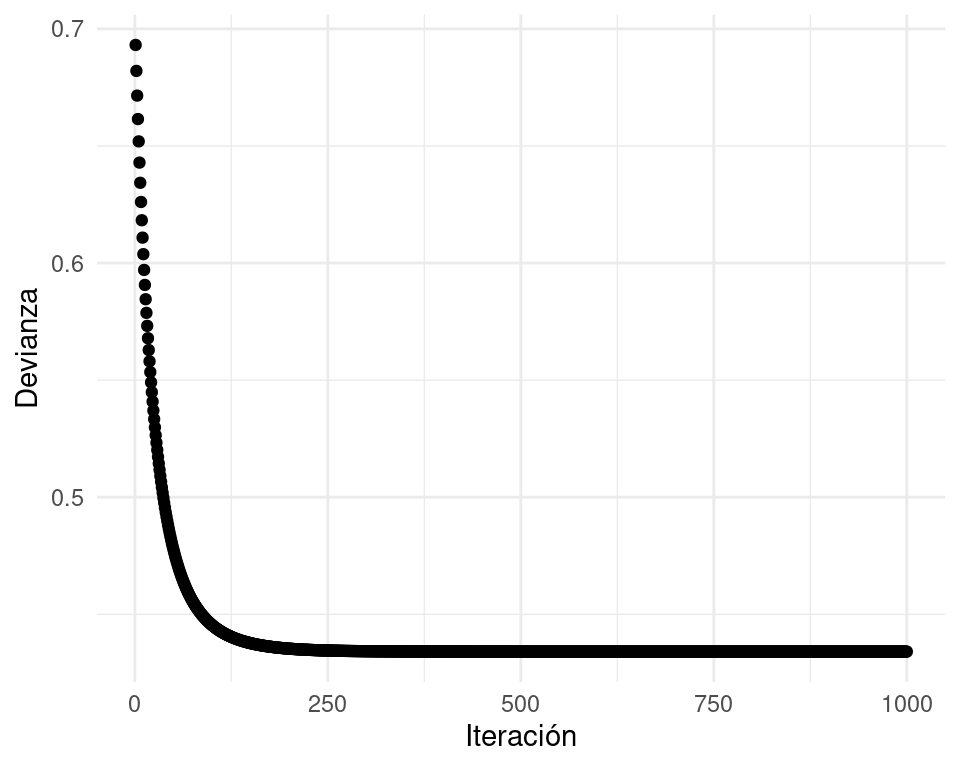
# Y gradiente de devianza en la iteración final:
grad(iteraciones[nrow(iteraciones), ])## Intercept x_s
## -6.253020e-06 4.518278e-06Comparamos con glm:
mod_1 <- glm(y ~ x_s, data = dat_ent, family = 'binomial')
coef(mod_1)## (Intercept) x_s
## 1.506007 -1.056707mod_1$deviance## [1] 434.0864log_perdida(iteraciones[200,])## [1] 0.435333La devianza que obtenemos con nuestros cálculos es:
mod_1$deviance / (2 * nrow(dat_ent))## [1] 0.4340864log_perdida(iteraciones[200,])## [1] 0.435333Máxima verosimilitud
Es fácil ver que este método de estimación de los coeficientes (minimizando la devianza de entrenamiento) es el método de máxima verosimilitud. La verosimilitud de la muestra de entrenamiento está dada por: \[L(\beta) =\prod_{i=1}^N p_{y^{(i)}} (x^{(i)})\] Y la log verosimilitud es \[l(\beta) =\sum_{i=1}^N \log(p_{y^{(i)}} (x^{(i)})).\] Así que ajustar el modelo minimizando la expresión (7.1) es los mismo que hacer máxima verosimilitud (condicional a los valores de \(x\)).
Normalización
Igual que en regresión lineal, en regresión logística conviene normalizar las entradas antes de ajustar el modelo
Desempeño de regresión logística como método de aprendizaje
Igual que en regresión lineal, regresión logística supera a métodos más sofisticados o nuevos en numerosos ejemplos. Las razones son similares: la rigidez de regresión logística es una fortaleza cuando la estructura lineal es una buena aproximación.
Solución analítica
El problema de regresión logística no tiene solución analítica. Paquetes como glm utilizan métodos numéricos (Newton-Raphson para regresión logística, por ejemplo).
Interpretación de modelos logísticos
Todas las precauciones que mencionamos en modelos lineales aplican para los modelos logísticos (aspectos estadísticos del ajuste, relación con fenómeno de interés, argumentos de causalidad). Igual que en regresión lineal, podemos explicar el comportamiento de las probabilidades de clase ajustadas, pero es un poco más difícil por la no linealidad introducida por la función logística.
Ejemplo
Consideremos el modelo ajustado:
head(dat_ent)## # A tibble: 6 × 4
## x g y x_s
## <dbl> <fct> <dbl> <dbl>
## 1 0.0240 al_corriente 1 -1.05
## 2 0.565 al_corriente 1 0.721
## 3 0.361 impago 0 0.0536
## 4 0.701 impago 0 1.17
## 5 0.128 al_corriente 1 -0.707
## 6 0.207 al_corriente 1 -0.450coeficientes <- iteraciones[200,]
names(coeficientes) <- c("Intercept", "x_s")
coeficientes## Intercept x_s
## 1.3766661 -0.9629202Como centramos todas las entradas, la ordenada al origen (Intercept) se interpreta como la probabilidad de clase cuando todas las variables están en su media:
options(digits = 2)
coeficientes[1]## Intercept
## 1.4h(coeficientes[1])## Intercept
## 0.8Esto quiere decir que la probabilidad de estar al corriente es de 80% cuando la variable \(x\) está en su media. Si \(x\) se incrementa en una desviación estándar, la cantidad \[z = \beta_0 + \beta_1x\] la probabilidad de estar al corriente cambia a 60%:
h(coeficientes[1]+ coeficientes[2]*1)## Intercept
## 0.6Nótese que una desviación estándar de \(x\) equivale a
sd(dat_ent$x)## [1] 0.31Así que en las unidades originales, un incremento de 0.31 en la variable \(x\) implica un cambio de
h(coeficientes[1] + coeficientes[2]) - h(coeficientes[1])## Intercept
## -0.2es decir, la probabilidad de manenterse al corriente baja 20 puntos porcentuales, de 80% a 60% Ojo: En regresión lineal, las variables contribuyen independientemente de otras al predictor. Eso no pasa en regresión logística debido a la no linealidad introducida por la función logística \(h\). Por ejemplo, imaginemos el modelo: \[p(z) = h(0.5 + 0.2 x_1 -0.5 x_2 + 0.7x_3),\] y suponemos las entradas normalizadas. Si todas las variables están en su media, la probabilidad de clase 1 es
h(0.5)## [1] 0.62Si todas las variables están en su media, y cambiamos en 1 desviación estándar la variable \(x_1\), la probabilidad de clase 1 es:
h(0.5 + 0.2)## [1] 0.67Y el cambio en puntos de probabilidad es:
h(0.5 + 0.2) - h(0.5)## [1] 0.046Pero si la variable \(x_2 = -1\), por ejemplo, el cambio en probabilidad es de
h(0.5 + 0.2 - 0.5 * (-1)) - h(0.5 - 0.5 * (-1))## [1] 0.03719.1 Ejercicio: datos de diabetes
Ya están divididos los datos en entrenamiento y prueba
diabetes_ent <- as_tibble(MASS::Pima.tr)
diabetes_pr <- as_tibble(MASS::Pima.te)
diabetes_ent## # A tibble: 200 × 8
## npreg glu bp skin bmi ped age type
## <int> <int> <int> <int> <dbl> <dbl> <int> <fct>
## 1 5 86 68 28 30.2 0.364 24 No
## 2 7 195 70 33 25.1 0.163 55 Yes
## 3 5 77 82 41 35.8 0.156 35 No
## 4 0 165 76 43 47.9 0.259 26 No
## 5 0 107 60 25 26.4 0.133 23 No
## 6 5 97 76 27 35.6 0.378 52 Yes
## 7 3 83 58 31 34.3 0.336 25 No
## 8 1 193 50 16 25.9 0.655 24 No
## 9 3 142 80 15 32.4 0.2 63 No
## 10 2 128 78 37 43.3 1.22 31 Yes
## # … with 190 more rowsdiabetes_ent$id <- 1:nrow(diabetes_ent)
diabetes_pr$id <- 1:nrow(diabetes_pr)Normalizamos
receta_diabetes <- recipe(type ~ ., diabetes_ent) |>
update_role(id, new_role = "id_variable") |>
step_normalize(all_predictors()) |>
prep()
diabetes_ent_s <- receta_diabetes |> juice()
diabetes_pr_s <- receta_diabetes |> bake(diabetes_pr)x_ent <- diabetes_ent_s |> select(-type, -id) |> as.matrix()
p <- ncol(x_ent)
y_ent <- diabetes_ent_s$type == 'Yes'
grad <- grad_calc(x_ent, y_ent)
iteraciones <- descenso(1000, rep(0,p+1), 0.1, h_deriv = grad)
matplot(iteraciones, type = "l")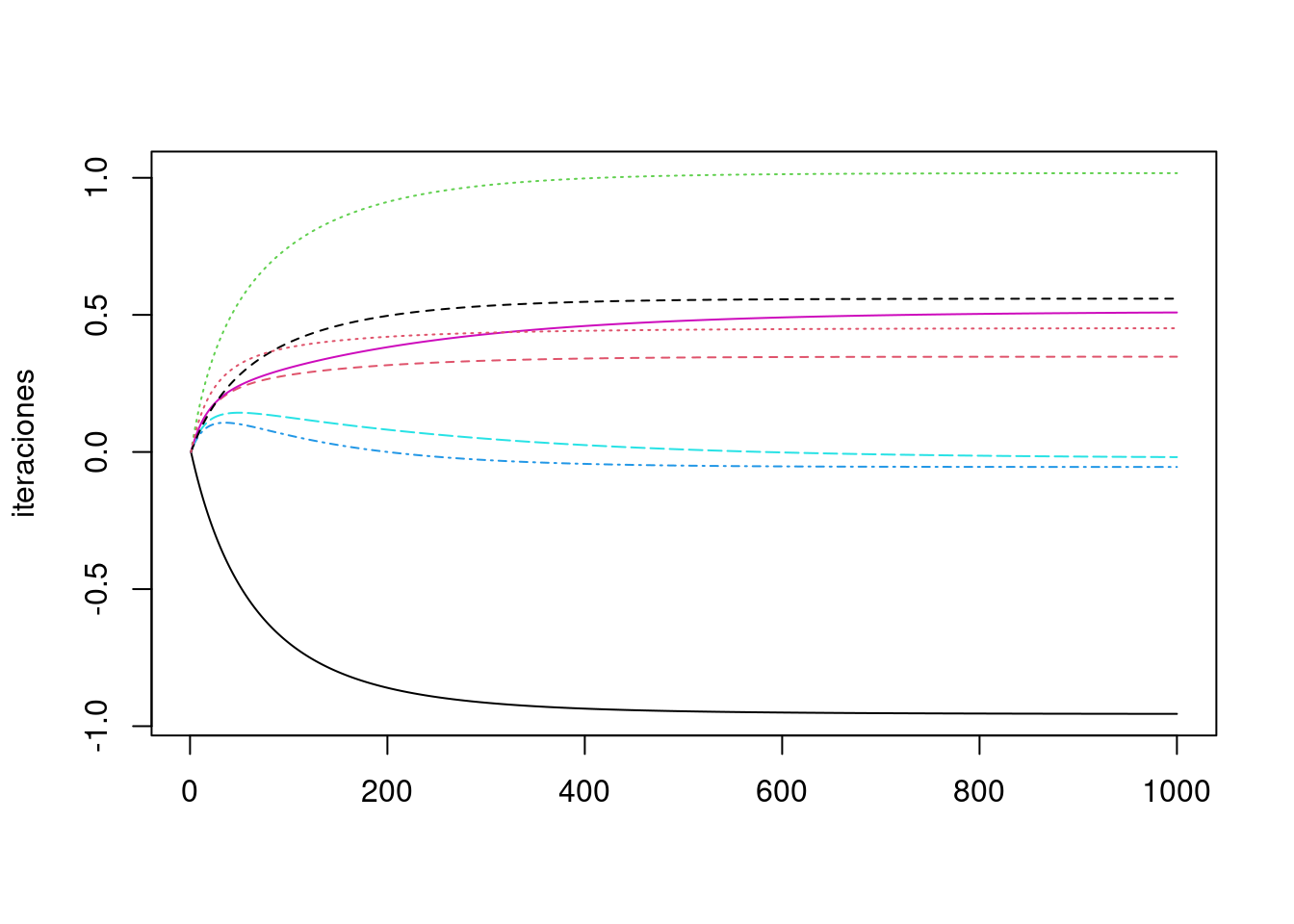
diabetes_coef <- tibble(variable = c('Intercept',colnames(x_ent)), coef = iteraciones[1000,])
diabetes_coef## # A tibble: 8 × 2
## variable coef
## <chr> <dbl>
## 1 Intercept -0.955
## 2 npreg 0.347
## 3 glu 1.02
## 4 bp -0.0547
## 5 skin -0.0187
## 6 bmi 0.509
## 7 ped 0.559
## 8 age 0.451Ahora calculamos devianza de prueba y error de clasificación:
x_prueba <- diabetes_pr_s |> select(-type, -id) |> as.matrix()
y_prueba <- diabetes_pr_s$type == 'Yes'
log_perdida_prueba <- log_perdida_calc(x_prueba, y_prueba)
log_perdida_prueba(iteraciones[1000,])## [1] 0.44Y para el error clasificación de prueba, necesitamos las probabilidades de clase ajustadas:
beta <- iteraciones[1000, ]
p_beta <- h(as.matrix(cbind(1, x_prueba)) %*% beta)
y_pred <- as.numeric(p_beta > 0.5)
mean(y_prueba != y_pred)## [1] 0.2Vamos a repetir usando keras.
library(keras)##
## Attaching package: 'keras'## The following object is masked from 'package:yardstick':
##
## get_weights# definición de estructura del modelo (regresión logística)
# es posible hacerlo con workflows como vimos arriba,
# pero aquí usamos directamente la interfaz de keras en R
n_entrena <- nrow(x_ent)
modelo_diabetes <- keras_model_sequential() |>
layer_dense(units = 1, #una sola respuesta,
activation = "sigmoid", # combinar variables linealmente y aplicar función logística
kernel_initializer = initializer_constant(0), #inicializamos coeficientes en 0
bias_initializer = initializer_constant(0)) #inicializamos ordenada en 0
# compilar seleccionando cantidad a minimizar, optimizador y métricas
modelo_diabetes |> compile(
loss = "binary_crossentropy", # devianza es entropía cruzada
optimizer = optimizer_sgd(lr = 0.75), # descenso en gradiente
metrics = list("binary_crossentropy"))
# Ahora iteramos
# Primero probamos con un número bajo de iteraciones
historia <- modelo_diabetes |> fit(
as.matrix(x_ent), # x entradas
y_ent, # y salida o target
batch_size = nrow(x_ent), # para descenso en gradiente
epochs = 20, # número de iteraciones
verbose = 0
)
plot(historia)## `geom_smooth()` using formula 'y ~ x'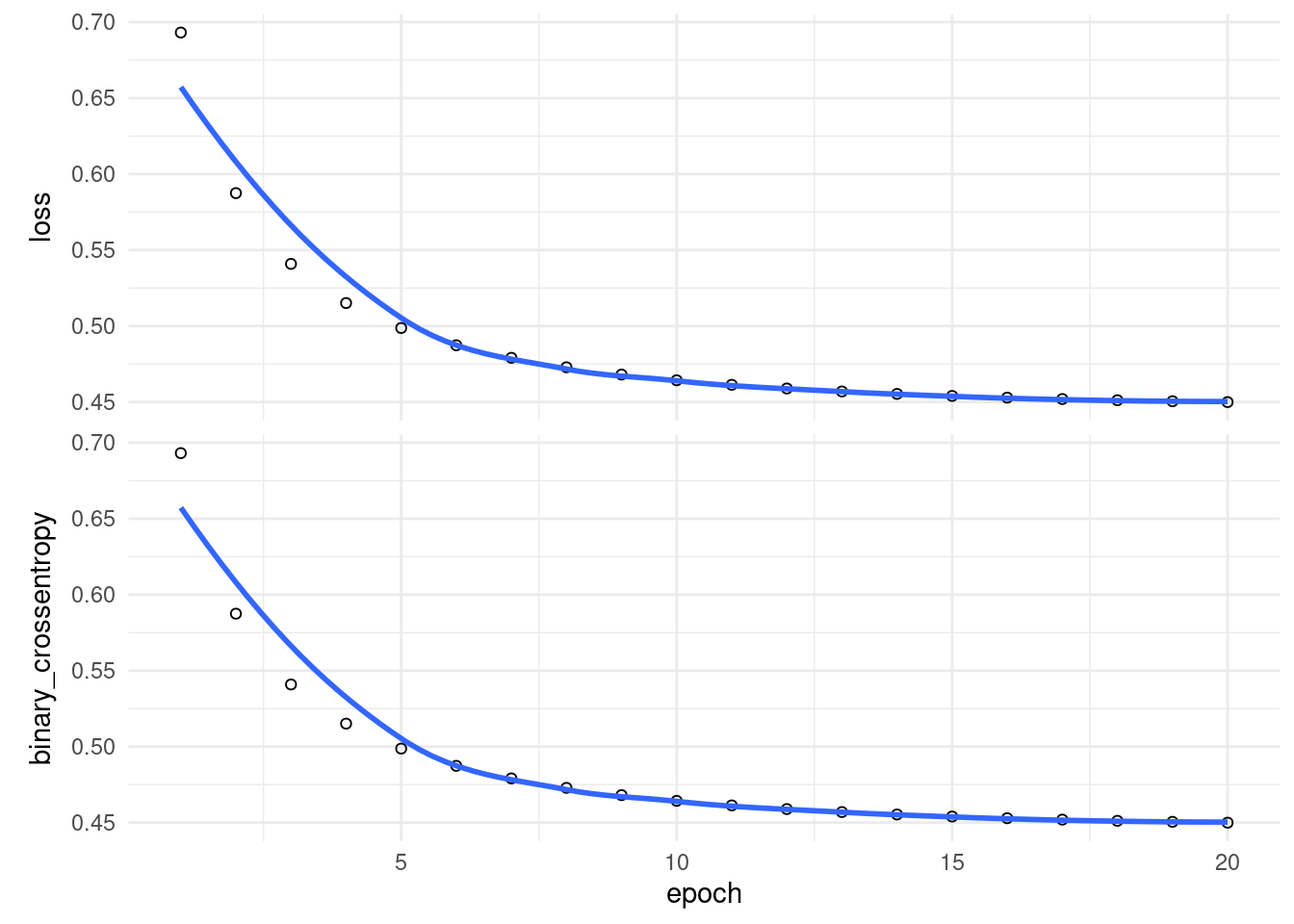
Y ahora podemos correr más iteraciones adicionales:
historia <- modelo_diabetes |> fit(
as.matrix(x_ent), # x entradas
y_ent, # y salida o target
batch_size = nrow(x_ent), # para descenso en gradiente
epochs = 400, # número de iteraciones
verbose = 0
)Los errores de entrenamiento y prueba son:
options(scipen = 0, digits = 4)
evaluate(modelo_diabetes, x_ent, y_ent)## loss binary_crossentropy
## 0.446 0.446evaluate(modelo_diabetes, x_prueba, y_prueba)## loss binary_crossentropy
## 0.4407 0.4407Veamos que coeficientes obtuvimos:
get_weights(modelo_diabetes)## [[1]]
## [,1]
## [1,] 0.34734
## [2,] 1.01705
## [3,] -0.05473
## [4,] -0.02247
## [5,] 0.51263
## [6,] 0.55927
## [7,] 0.45201
##
## [[2]]
## [1] -0.9558Y comparamos con lo que obtenemos de glm:
# podemos hacerlo con workflows, como vimos arriba.
# aquí usamos directamente la interfaz de glm en R
mod_1 <- glm(type ~ ., diabetes_ent_s |> select(-id), family = binomial())
mod_1 |> coef()## (Intercept) npreg glu bp skin bmi
## -0.95583 0.34734 1.01705 -0.05473 -0.02247 0.51263
## ped age
## 0.55928 0.45201