Clase 6 Incertidumbre en las predicciones
En todos los casos hasta ahora, vimos cómo hacer:
- Predicciones puntuales (un solo valor)
- Evaluar un conjunto razonablemente grande de predicciones con el error de predicción, que es un promedio de la pérdida seleccionada.
Este enfoque es razonable en algunos casos y otros no. Es razonable cuando:
- el error de predicción es relativamente chico (tenemos predicciones muy precisas). Entonces cualquier pérdida usual que utilicemos funciona apropiadamente.
- Los errores son poco costosos, especialmente si comparamos con la mejoría en la automatización del proceso.
Un ejemplo del primer caso es el de la lectura de medidores: en este caso, nuestro modelo es bastante preciso y las predicciones puntuales son suficientes. Un ejemplo del segundo caso es hacer recomendaciones de películas o productos: la automatización en el proceso presenta buenas ganancias, y recomendar una película incorrecta no es grave mientras que en promedio tengamos buenos aciertos.
Sin embargo, muchos problemas de predicción no son así, y el error juega un papel importante:
- Los errores pueden ser relativamente grandes, de forma que dada una predicción, el valor observado puede producir costos grandes.
- Nuestras predicciones van a usarse downstream para tomar una serie de decisiones que no conocemos de antemano, y en consecuencia la estructura de costos de un error es compleja y sólo parcialmente definida. Ninguna pérdida usual refleja correctamente el costo-beneficio de usar un modelo.
Ejemplos del primero puede ser el de predicción de precios de casas: errores de 20% en el precio puede convertir una compra deseable en una que produce pérdidas grandes. En el segundo, un ejemplo es la estimación futura de compras de un cliente (asociado al valor presente de los clientes o usuarios): dependiendo de esta estimación puede ser que tomemos una serie de decisiones distintas acerca de productos, promociones, etc. (no definidos de antemano generalmente) para ofrecer que tienen consecuencias considerables. Otro ejemplo es predecir si en una tomografía hay evidencia de cáncer: aún cuando la probabilidad de que sea una imagen “normal” es alta (digamos 75%), una probablidad de 25% de que sea cancerígena debe ser puesta frente a los tomadores de decisiones.
En todos estos casos, es importante producir alguna cuantificación de la incertidumbre en lugar de una predicción puntual solamente (un solo precio, o una sola categoría “Normal”). Esta cuantificación puede ofrecerse a los tomadores de decisiones, y puede utilizarse también en simulaciones de decisiones tomadas downstream.
Una manera básica de cuantificar la incertidumbre es construir intervalos predictivos. En lugar de producir una predicción puntual \(\hat{f}(x)\), producimos dos valores \([\hat{q}_1(x), \hat{q}_2(x)]\) donde es probable que caiga el valor observado \(y\). Por ejemplo, si construimos intervalos del 90%, quisiéramos entonces que se cumpla la garantía de cobertura siguiente: \[P(\mathbf{y}\in [\hat{q}_1(\mathbf{x}), \hat{q}_2(\mathbf{x})]) = 0.90\] donde la probabilidad es tomada sobre toda la población \((\mathbf{x}, \mathbf{y})\) de interés. Por ejemplo, para el precio de una casa, en lugar de producir una sola predicción de 120 mil dólares, produciríamos un intervalo de 50 a 180 mil dólares. Eso nos pone en una situación considerablemente distinta que si el intervalo fuera de 110 a 130 mil dólares, por ejemplo para una decisión de una compañía de bienes raíces.
6.1 Inferencia predictiva conforme
Tradicionalmente, este tipo de intervalos predictivos se construyen bajo argumentos teóricos en modelos relativamente simples con supuestos fuertes que hay que checar. En aprendizaje de máquina, donde utilizamos predictores mucho más complejos que modelos lineales, en dimensión alta y con mecanismos complejos de limpieza y selección de variables, es muy difícil seguir esta ruta tradicional.
En lugar de eso, utilizaremos la idea fundamental de división de muestras (entrenamiento -prueba) para producir intervalos con cobertura garantizada independientemente de si se cumplen o no ciertos supuestos teóricos. La idea es la siguiente:
Intervalos predictivos con muestra de prueba.
Suponiendo que los datos se extraen de forma independiente de una misma población,
- Construimos con una muestra de entrenamiento \((x_i, y_i)\) nuestro predictor \(\hat{f}(x)\)
- Usamos una muestra de prueba separada para evaluar el error promedio, y adicionalmente, calculamos los valores \(\mathbf{r}_i = |\mathbf{y}_i - \hat{f}(\mathbf{x}_i)|\)
- Si queremos intervalos del 90%, calculamos ahora \(q\), que es el cuantil 90% de los valores \(\mathbf{r}_i\)
- Para un nuevo valor de las entradas \(\mathbf{x}\), nuestro intervalo es \[[\hat{f}(\mathbf{x}) - d, \hat{f}(\mathbf{x}) + d]\]
Para esta nueva observación \((\mathbf{x}, \mathbf{y})\),
\[P(\mathbf{y} \in[\hat{f}(\mathbf{x}) - d, \hat{f}(\mathbf{x}) + d])\gtrsim 0.90\]
donde la desigualdad quiere decir que la cobertura es al menos de 90%, y muy cercana a 90% si la muestra de prueba cumple \(n\geq 100\).La demostración es relativamente simple (especialmente el hecho de que la cobertura es mayor o igual a 90%) y no requiere ningún supuesto adicional acerca del predictor o al calidad del ajuste (ver Distribution-Free Predictive Inference for Regression).
6.2 Ejemplo: bodyfat
En el ejemplo de grasa corporal utilizamos lasso para seleccionar un modelo. Podemos construir intervalos predictivos (split-conformal) como sigue:
library(tidyverse)
library(tidymodels)
library(gt)
dat_grasa <- read_csv(file = '../datos/bodyfat.csv')
set.seed(183)
grasa_particion <- initial_split(dat_grasa, 0.5)
grasa_ent <- training(grasa_particion)
grasa_pr <- testing(grasa_particion)
grasa_receta <- recipe(grasacorp ~ ., grasa_ent)
# lasso
modelo_gc <- linear_reg(mixture = 1, penalty = 1.5) %>%
set_engine("glmnet", lambda.min.ratio = 1e-20)
flujo_2 <- workflow() %>%
add_model(modelo_gc) %>%
add_recipe(grasa_receta)
# ajuste
flujo_2 <- flujo_2 %>% fit(grasa_ent)Ahora, sobre la muestra de prueba evaluamos el error y calculamos residuales y su distribución:
preds_gc_tbl <- predict(flujo_2, grasa_pr) |>
bind_cols(grasa_pr) |>
mutate(residual = abs(grasacorp - .pred))
ggplot(preds_gc_tbl, aes(x = residual)) +
geom_histogram(binwidth = 2)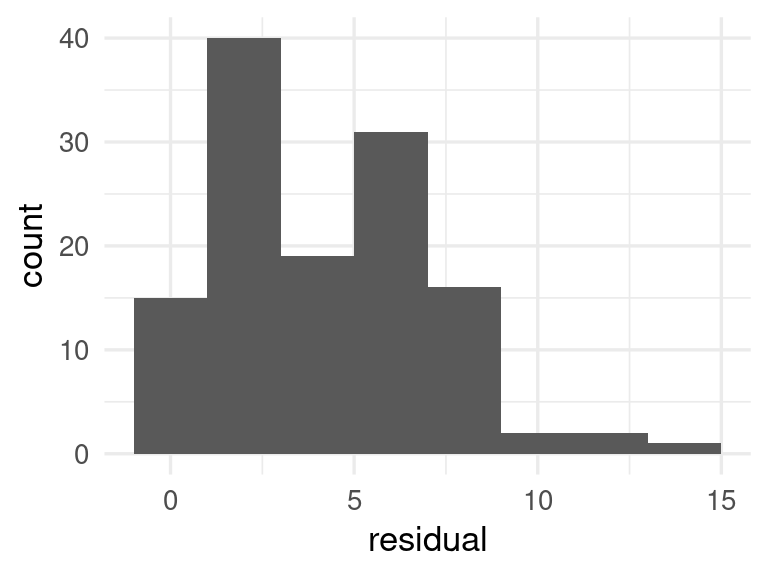
q_gc <- quantile(preds_gc_tbl |> pull(residual), probs = c(0.90))
q_gc |> round(2)## 90%
## 8.13Y finalmente, podemos hacer distintas verificaciones para ver cómo se comportan los residuales, por ejemplo:
preds_gc_tbl <- preds_gc_tbl |>
mutate(inf = .pred - q_gc, sup = .pred + q_gc)
ggplot(preds_gc_tbl, aes(x = abdomen, ymin = inf, ymax = sup, y = grasacorp)) +
geom_point(colour = "red") +
geom_linerange()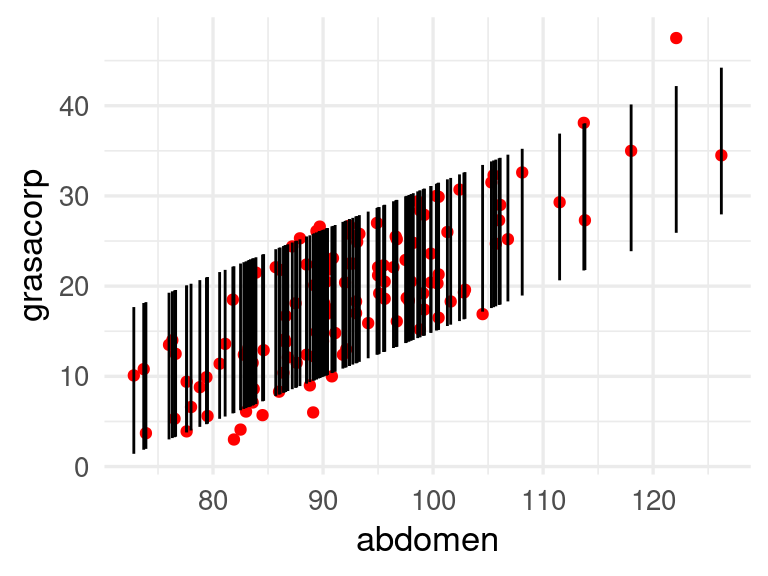
Una gráfica útil es la de predicciones en la escala de las \(x\) contra intervalos y observados en el eje \(y\).
ggplot(preds_gc_tbl, aes(x = .pred, ymin = inf, ymax = sup, y = grasacorp)) +
geom_abline() +
geom_point(colour = "red") +
geom_linerange(alpha = 0.5) 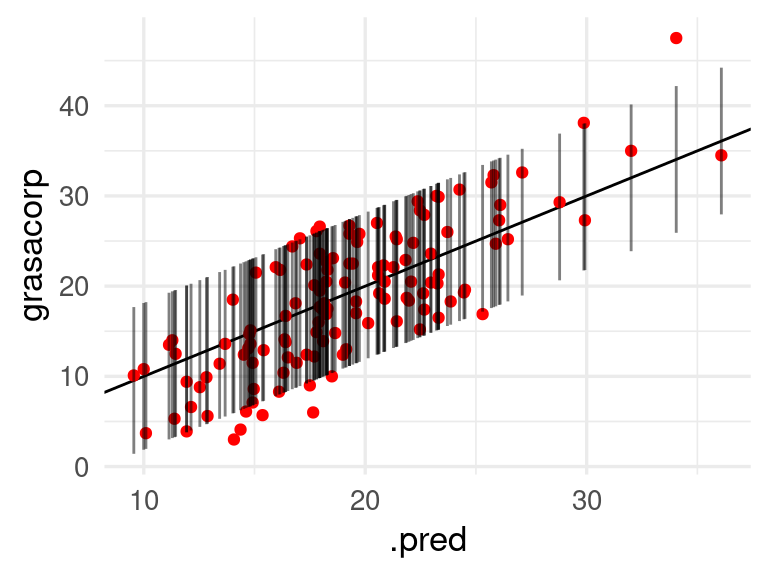
Donde vemos que la cobertura parece ser similar para todos los rangos de valores de predicción. Podemos hacer también una tabla simple como la que sigue para verificar la cobertura:
n_grupos <- 4 # podemos usar más grupos si tenemos más datos
preds_gc_tbl |>
rename(y = grasacorp) |>
mutate(grupo_pred = cut_number(.pred, n = n_grupos)) |>
group_by(grupo_pred) |>
summarise(n = n(), cobertura = mean(y >= inf & y <= sup)) |>
mutate(error_cob = 2 * sqrt(cobertura * (1- cobertura) / n)) |>
gt() |> fmt_number(where(is_double), decimals = 2)| grupo_pred | n | cobertura | error_cob |
|---|---|---|---|
| [9.55,16.1] | 32 | 0.88 | 0.12 |
| (16.1,18.4] | 31 | 0.84 | 0.13 |
| (18.4,22.3] | 31 | 0.97 | 0.06 |
| (22.3,36.1] | 32 | 0.91 | 0.10 |
6.3 Defectos de los intervalos simples predictivos conformes
La cobertura es confiable y robusta, sin embargo, se requieren algunos elementos adicionales para que los intervalos sean más útiles. Quisiéramos también que la cobertura local alrededor de cualquier región del las \(x\)’s sea cercana al 90% (cobertura condicional). Esto es más dificíl de alcanzar.
Un chequeo básico que podemos hacer es el siguiente:
- Para cada nivel de predicción \(\hat{y} = \hat{f}(x)\), los intervalos tienen cobertura de 90%.
Como esto sólo involucra las predicciones, los valores observados, y los intervalos predictivos, esto puede checarse en la práctica con una tabla o gráfica. En caso de que no se cumpla esta condición, podemos usar una muestra independiente adicional de calibración, y mejorar esta cobertura condicional.
Finalmente, a veces es importante que los intervalos tengan cobertura similar a lo largo de distintos valores de algunas entradas \(x_i\) particulares. Por ejemplo, si \(x_i\) indica nivel socioeconómico de un hogar, no quisiéramos introducir artefactos en la decisión debido a que la cobertura es desigual para distintos valores de esta variable de entrada.
6.4 Ejemplo: rendimiento
Revisamos nuestro ejemplo de rendimiento de coches:
library(tidyverse)
library(tidymodels)
library(gt)
auto <- read_csv("../datos/auto.csv")
datos <- auto[, c('name', 'weight','year', 'mpg', 'displacement')]
datos <- datos %>% mutate(
peso_kg = weight * 0.45359237,
rendimiento_kpl = mpg * (1.609344 / 3.78541178),
año = year)Vamos a separa en muestra de entrenamiento y de prueba estos datos. Podemos hacerlo como sigue (75% para entrenamiento aproximadamente en este caso, así obtenemos alrededor de 100 casos para prueba):
set.seed(121)
datos_split <- initial_split(datos, prop = 0.3)
datos_entrena <- training(datos_split)
datos_prueba <- testing(datos_split)
# preprocesamiento y flujo
receta_lineal <- recipe(rendimiento_kpl ~ peso_kg + año, datos_entrena) |>
step_ns(peso_kg, deg_free = 3) |>
step_ns(año, deg_free = 2)
mod_lineal <- linear_reg() |>
set_engine("lm")
flujo <- workflow() |>
add_recipe(receta_lineal) |>
add_model(mod_lineal)
flujo_ajustado <- fit(flujo, datos_entrena)Una vez que tenemos el flujo ajustado, podemos ver cómo se comportan los residuales:
preds_tbl <- predict(flujo_ajustado, datos_prueba) |>
bind_cols(datos_prueba) |>
mutate(r = abs(rendimiento_kpl - .pred))
ggplot(preds_tbl, aes(x = r)) + geom_histogram()## `stat_bin()` using `bins = 30`. Pick better value with `binwidth`.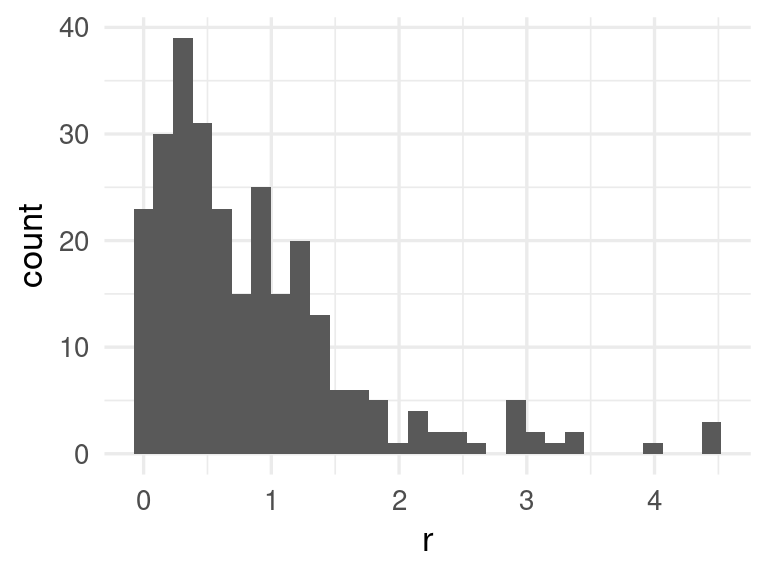
q <- quantile(preds_tbl |> pull(r), probs = c(0.90)) |>
round(2)
q## 90%
## 1.77Podemos ahora construir intervalos de 90% para nuestras predicciones de la siguiente forma:
preds_tbl <- preds_tbl |>
mutate(inf = .pred - q,
sup = .pred + q)Por definición, estos intervalos tienen cobertura promedio sobre nuevos datos de aproximadamente el 90%.
Sin embargo, la cobertura puede nos ser uniforme en distintas regiones de las entradas. Como sugerimos arriba, podemos checar primero la respuesta en función de la predicción:
ggplot(preds_tbl, aes(x = .pred, y = rendimiento_kpl, ymin = inf, ymax = sup)) +
geom_linerange() +
geom_point(colour = "red") + coord_obs_pred()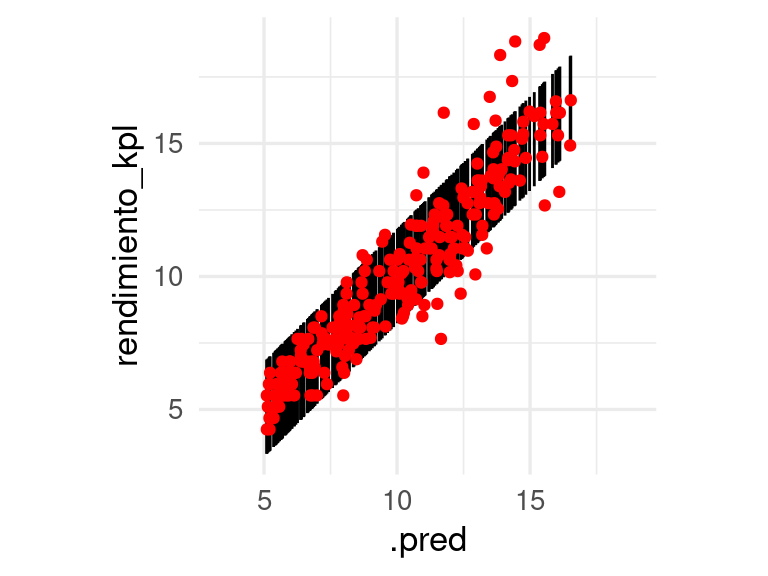
También podemos verificar con una tabla que la cobertura no es uniforme:
n_grupos <- 6 # podemos usar más grupos si tenemos más datos
preds_tbl |>
rename(y = rendimiento_kpl) |>
mutate(grupo_pred = cut_number(.pred, n = n_grupos)) |>
group_by(grupo_pred) |>
summarise(n = n(), cobertura = mean(y >= inf & y <= sup)) |>
mutate(error_e = 2 * sqrt(cobertura * (1- cobertura) / n)) |>
gt() |> fmt_number(where(is_double), decimals = 2)| grupo_pred | n | cobertura | error_e |
|---|---|---|---|
| [5.1,6.46] | 46 | 1.00 | 0.00 |
| (6.46,8.08] | 46 | 0.98 | 0.04 |
| (8.08,10.1] | 46 | 0.93 | 0.07 |
| (10.1,11.6] | 45 | 0.89 | 0.09 |
| (11.6,13.6] | 46 | 0.78 | 0.12 |
| (13.6,16.5] | 46 | 0.83 | 0.11 |
Estos intervalos son poco útiles porque exageran la incertidumbre para valores altos y la subestiman para valores bajos.
Adicionalmente, podemos checar variables que consideramos importantes para ver cómo se comportan los intervalos. En este caso, por ejemplo, usamos la variable peso,
ggplot(preds_tbl, aes(x = peso_kg, y = rendimiento_kpl, ymin = inf, ymax = sup)) +
geom_linerange() +
geom_point(colour = "red") 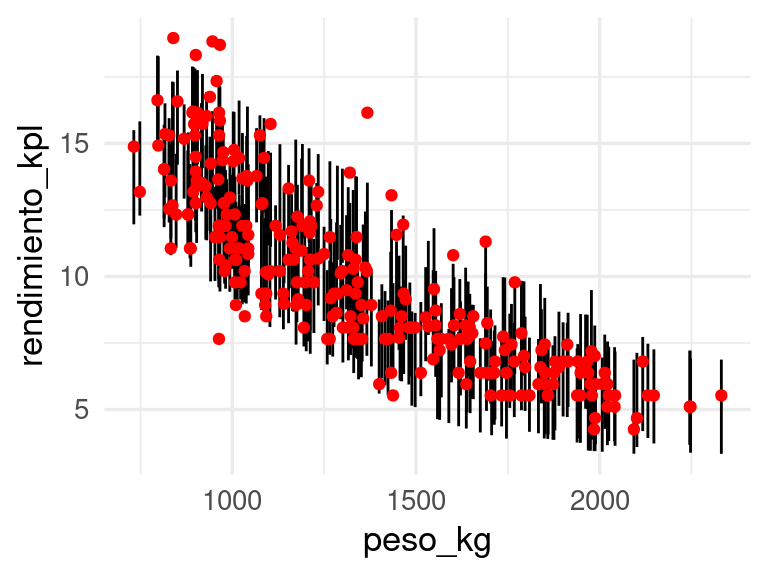
Y vemos que aunque nuestros intervalos son del 90%, tienen baja cobertura para pesos bajos y sobrecubren para pesos altos.
Podemos mejorar los intervalos usando regresión cuantílica, donde la respuesta es la variable que queremos predecir y la única entrada es nuestra predicción puntual. Primero necesitamos una muestra adicional de calibración (por ejemplo dividimos la muestra de prueba en una muestra de calibración y otra de evaluación):
lambda <- 1 # suavizamiento splines reg cuantílica
calib_eval_split <- initial_split(preds_tbl, 0.5)
calibracion_tbl <- training(calib_eval_split)
eval_tbl <- testing(calib_eval_split)
ggplot(calibracion_tbl, aes(x = .pred, y = rendimiento_kpl)) +
geom_point() +
geom_quantile(method = "rqss", lambda = lambda, quantiles = c(0.05, 0.95))## Smoothing formula not specified. Using: y ~ qss(x, lambda = 1)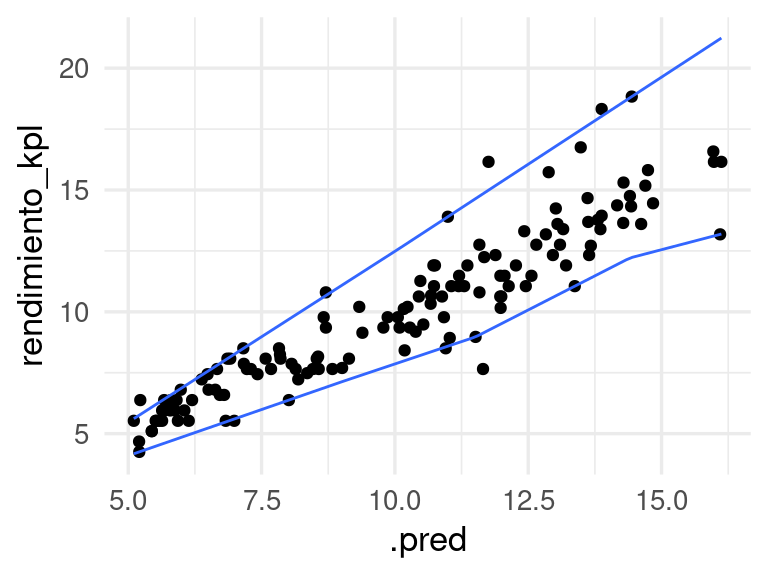
sup_qreg <- quantreg::rqss(rendimiento_kpl ~ .pred, lambda = lambda, data = preds_tbl, tau = 0.95)
inf_qreg <- quantreg::rqss(rendimiento_kpl ~ .pred, lambda = lambda, data = preds_tbl, tau = 0.05)
calibracion_tbl <- calibracion_tbl |>
mutate(sup_q = predict(sup_qreg, newdata = calibracion_tbl),
inf_q = predict(inf_qreg, newdata = calibracion_tbl))Los nuevos intervalos se ven como sigue, por ejemplo en términos de la variable peso:
ggplot(calibracion_tbl, aes(x = peso_kg, y = rendimiento_kpl, ymin = inf_q, ymax = sup_q)) +
geom_linerange() +
geom_point(colour = "red") 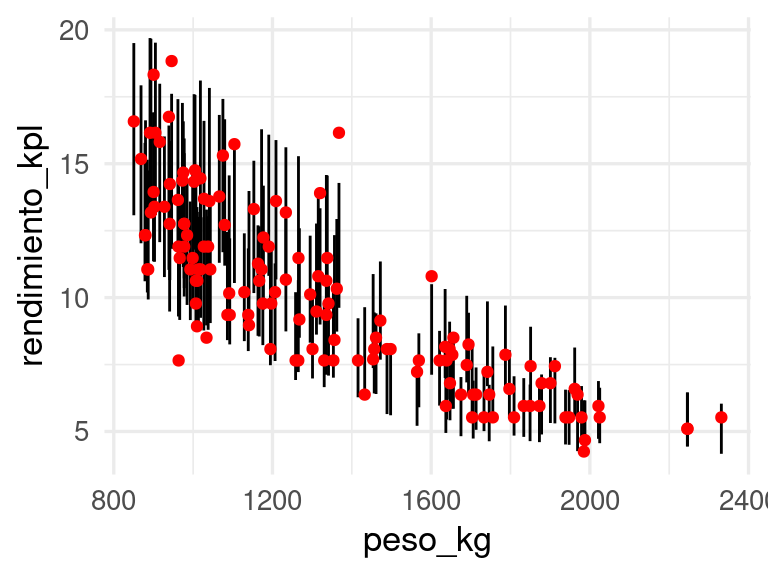
Finalmente verificamos con la muestra de evaluación (en este punto, podemos ajustar la regresión cuantílica si es necesario):
eval_tbl <- eval_tbl |>
mutate(sup_q = predict(sup_qreg, newdata = eval_tbl),
inf_q = predict(inf_qreg, newdata = eval_tbl))n_grupos <- 5 # podemos usar más grupos si tenemos más datos
eval_tbl |>
rename(y = rendimiento_kpl) |>
mutate(grupo_pred = cut_number(.pred, n = n_grupos)) |>
group_by(grupo_pred) |>
summarise(n = n(), cobertura = mean(y >= inf_q & y <= sup_q), .pred = mean(.pred)) |>
mutate(error_cob = 2 * sqrt(cobertura * (1- cobertura) / n)) |>
ggplot(aes(x = .pred, y = cobertura, ymin = cobertura - error_cob, ymax = cobertura + error_cob)) +
geom_hline(yintercept = 0.9, colour = "red") +
geom_point() + geom_linerange() +
ylim(c(0,1.1))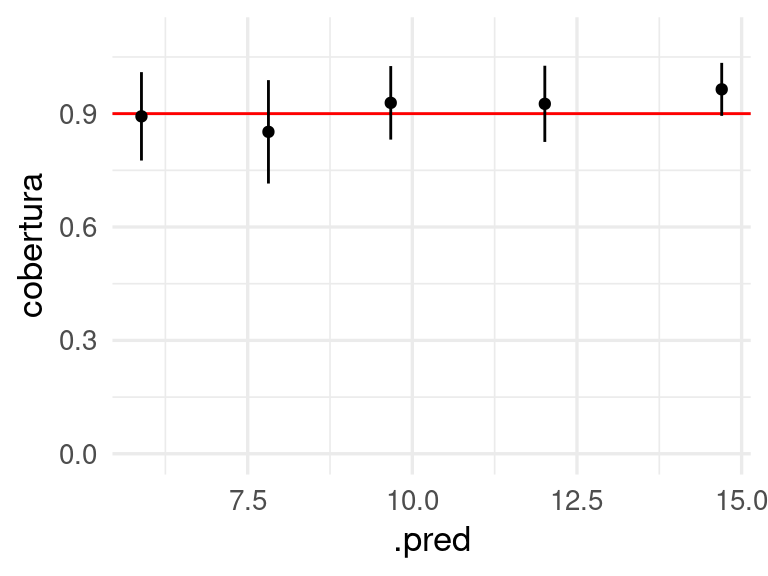
Probando intervalos predictivos
- Checamos la cobertura uniforme de nuestros intervalos predictivos primero viendo el comportamiento de intervalos dependiendo de la predicción.
- Adicionalmente, podemos también checar intervalos en función de variables importantes para ver si en distintas regiones la cobertura es uniforme.
- Cuando detectamos que los intervalos predictivos conformes no tienen niveles de cobertura uniforme sobre el espacio de entradas, podemos usar una muestra de calibración y usar regresión cuantílica tomando como respuesta la variable respuesta y como entrada la predicción puntual de nuestro modelo ajustado.
6.5 Ejemplo: otras funciones de pérdida
El mismo método puede aplicarse para otras funciones de pérdida más apropiadas para cada problema. Supongamos que en el problema de predicción de precios, nos interesa particularmente la pérdida relativa dada por
\[L(y, \hat{f}(x)) = \frac{|y - \hat{f}(x)|}{\hat{f}(x)}\]
En este caso, a la pérdida \(L(y, \hat{f}(x))\) a veces se le llama medida de conformidad de las predicciones. Podemos aplicar entonces el mismo procedimiento:
- Construimos con una muestra de entrenamiento \((x_i, y_i)\) nuestro predictor \(\hat{f}(x)\)
- Usamos una muestra de prueba separada para evaluar el error promedio, y adicionalmente, calculamos los valores \(\mathbf{r}_i = L(\mathbf{y}_i , \hat{f}(\mathbf{x}_i))\)
- Si queremos intervalos del 90%, calculamos ahora \(q\), que es el cuantil 90% de los valores \(\mathbf{r}_i\)
- Para un nuevo valor de las entradas \(\mathbf{x}\), nuestro intervalo ( o más bien región predictiva) es todos los valores de \(y\) que cumplen \[I(\mathbf{x}) = \{y : L(y, \hat{f}(\mathbf{x})) \leq q\} \] Y resulta ser que para una nueva observación,
\[P(\mathbf{y} \in I(\mathbf{x}))\gtrsim 0.90\] Podemos ver esto con el ejemplo de precios de casas:
source("../R/casas_traducir_geo.R")
set.seed(83)
casas_split <- initial_split(casas, prop = 0.75)
casas_entrena <- training(casas_split)
receta_casas <- recipe(precio_miles ~
nombre_zona +
area_hab_m2 + area_garage_m2 + area_sotano_m2 +
area_2o_piso_m2 +
area_lote_m2 +
año_construccion +
calidad_gral + calidad_garage + calidad_sotano +
condicion_gral +
num_coches +
aire_acondicionado + condicion_venta,
data = casas_entrena) |>
step_filter(condicion_venta == "Normal") |>
step_select(-condicion_venta, skip = TRUE) |>
step_mutate(tiene_2o_piso = ifelse(area_2o_piso_m2 == 0, 1, 0)) |>
step_mutate(area_sotano_m2 = ifelse(is.na(area_sotano_m2), 0, area_sotano_m2)) |>
step_mutate(area_garage_m2 = ifelse(is.na(area_garage_m2), 0, area_garage_m2)) |>
step_novel(nombre_zona, calidad_sotano, calidad_garage) |>
step_ns(calidad_gral, deg_free = 2) |>
step_ns(condicion_gral, deg_free = 2) |>
step_ns(starts_with("area_lote"), deg_free = 3) |>
step_ns(starts_with("año_construccion"), deg_free = 3) |>
step_unknown(calidad_sotano, calidad_garage) |>
step_other(nombre_zona, threshold = 0.01, other = "otras") |>
step_dummy(nombre_zona, calidad_garage, calidad_sotano, aire_acondicionado) |>
step_interact(terms = ~ starts_with("area_garage_m2"):starts_with("calidad_garage")) |>
step_interact(terms = ~ starts_with("area_sotano_m2"): starts_with("calidad_sotano")) |>
step_nzv(all_predictors(), freq_cut = 500 / 1, unique_cut = 1)Usaremos regresión ridge:
flujo_casas <- workflow() |>
add_recipe(receta_casas) |>
add_model(linear_reg(mixture = 0, penalty = 0.01) |>
set_engine("glmnet", lambda.min.ratio = 1e-20))
ajuste <- fit(flujo_casas, casas_entrena)Para medir el desempeño convertimos a la variable de precio multiplicando la predicción por el área habitable:
metricas <- metric_set(mape, mae, rmse, rsq)
casas_prueba_normal <- testing(casas_split) |>
filter(condicion_venta == "Normal")
metricas(casas_prueba_normal |> bind_cols(predict(ajuste, casas_prueba_normal)),
truth = precio_miles, estimate = .pred ) |>
gt() |> fmt_number(.estimate, decimals = 2)| .metric | .estimator | .estimate |
|---|---|---|
| mape | standard | 9.05 |
| mae | standard | 15.25 |
| rmse | standard | 20.54 |
| rsq | standard | 0.92 |
La distribución de los residuales (que en este caso se llaman maś bien valores de conformidad) se ve como sigue:
preds_tbl <- casas_prueba_normal |>
bind_cols(predict(ajuste, casas_prueba_normal)) |>
mutate(residual = abs(precio_miles - .pred)/.pred)
preds_tbl |> ggplot(aes(x = residual)) + geom_histogram()## `stat_bin()` using `bins = 30`. Pick better value with `binwidth`.
q <- quantile(preds_tbl$residual, 0.90)set.seed(832)
preds_tbl <- preds_tbl |>
mutate(inf = .pred *(1 - q), sup = .pred *(1 + q)) |>
mutate(pred_precio = .pred ) |>
mutate(inf_precio = inf, sup_precio = sup)
ggplot(preds_tbl, aes(x = pred_precio, y = precio_miles, ymin = inf_precio,
ymax = sup_precio)) +
geom_abline() +
geom_linerange() +
geom_point(colour = "red") + coord_obs_pred()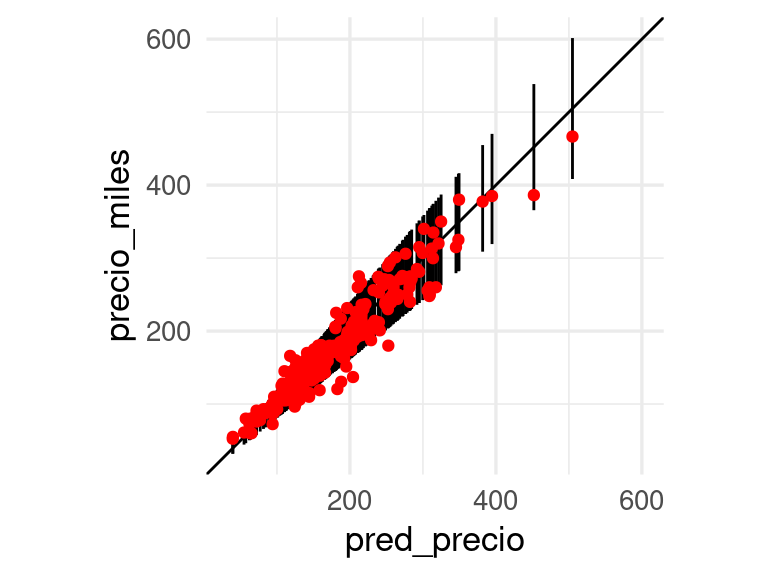
Checamos finalmente que la calibración es razonable con una tabla:
n_grupos <- 10 # podemos usar más grupos si tenemos más datos
preds_tbl |>
rename(y = precio_miles) |>
mutate(grupo_pred = cut_number(pred_precio, n = n_grupos)) |>
group_by(grupo_pred) |>
summarise(n = n(), cobertura = mean(y >= inf_precio & y <= sup_precio),
pred_precio = mean(pred_precio)) |>
mutate(error_cob = 2 * sqrt(cobertura * (1- cobertura) / n)) |>
ggplot(aes(x = pred_precio, y = cobertura, ymin = cobertura - error_cob, ymax = cobertura + error_cob)) +
geom_hline(yintercept = 0.9, colour = "red") +
geom_point() + geom_linerange() + ylim(c(0.5, 1.1))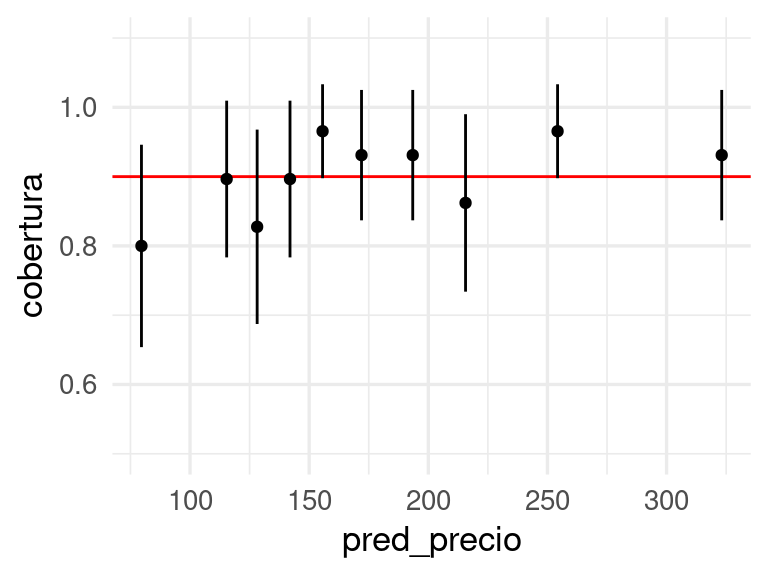
6.6 Resumen
- Los intervalos conformes producidos aquí tienen garantías de cobertura promedio, pero no necesariamente condicional a valores de \(x\) particulares.
- El chequeo básico consiste en ver cómo se comporta la cobertura para distintos valores de la predicción.
- Cuando un atributo \(x\) es importante (por ejemplo por razones de discriminación, o razones de negocio), podemos checar la cobertura condicional a \(x\) (como en el ejemplo de grasa corporal de arriba).
- Cuando la cobertura condicional no se cumple, podemos usar una muestra adicional para calibrar los intervalos. Esto se puede hacer ad-hoc o usando regresión cuantílica.
- Una alternativa adicional que se puede utilizar es intentar estimar directamente los cuantiles de la respuesta (por ejemplo 5 y 95% para un intervalo del 90%). Existe una función de pérdida diseñada para este propósito (veremos más adelante) que se puede aplicar a regresión lineal, redes neuronales, métodos basados en árboles y otros. Igualmente, es necesario checar y calibrar si es necesario los intervalos resultantes.
- La selección de medida de conformidad (o función de pérdida) para cada modelo no es trivial, y de esa medida depende el comportamiento de los intervalos. En problemas de regresión, pérdida absoluta y MAPE (error porcentual absoluto promedio) son usuales, y una puede desempeñarse mejor que otra.